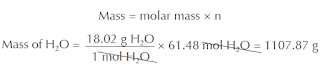Aviation has come a long way since the first balloon flights more than 200 years ago. Enormous advances in chemistry and physics have made it possible for humans to develop technologies needed for flying and even living in space. Today, rotating teams of astronauts live and work inside the International Space Station (ISS), and have kept it running since 1998.
Many challenges faced the designers of the ISS, and a lot of questions had to be answered before humans could safely live on the space station. Since there is no oxygen in space, a method for generating oxygen for the astronauts to breathe had to be developed. In this section, you will learn how a chemical reaction can be applied to produce oxygen in just the right quantities for human use on the ISS. Figure 20 The oxygen necessary for astronaut survival is produced via
a chemical reaction on board the International Space Station.
Molecular Mass
Before we discuss how chemical reactions can be used to produce needed amounts of substances, we must establish some important relationships in chemical terms. One of these is molecular mass, which is defined as the mass of one molecule.
Three molecules are represented below. Do you think that they all have the same mass? The answer is no, because they contain different numbers of atoms representing elements that differ in mass.
Figure 21 Structural formulas of water molecule (a), fluorine molecule (b), and carbon tetrachloride molecule (c)
You can calculate the molecular mass of each of these molecules by adding the relative atomic masses of all atoms in the molecule.
Note that when there are multiple atoms of the same element in a molecule, the mass of each atom is counted. A molecule of water contains two hydrogen atoms, and each contributes 1.01 amu to the mass of the molecule. Therefore, the mass of hydrogen is multiplied by two to account for this.
Thus, the molecular mass for water is:
atomic mass of oxygen + 2(atomic mass of hydrogen) = molecular mass of water
16.00 + 2 × 1.01 = 18.02
Therefore, the mass of one molecule of water is 18.02 amu.
Note that molecular mass is more properly denoted as relative molecular mass, which is unitless because it is the sum of relative atomic masses (which are also unitless). However, relative molecular mass is more commonly known as molecular mass. Although molecular masses are unitless, the mass of one molecule is expressed in amu.
Another example is carbon tetrachloride, CCl4. The molecular mass is calculated as shown below.
atomic mass of carbon + 4(atomic mass of chlorine) = molecular mass of carbon tetrachloride
12.01 + 4 × 35.45 = 153.81
Therefore, the mass of one molecule of CCl4 is 153.81 amu.
Molar Mass
You have just learned how to calculate molecular mass, which allows you to know the mass of one molecule. However, in the lab, a chemist would not typically work with a single molecule. Suppose that a chemist had one mole of carbon tetrachloride. The mass of one molecule of carbon tetrachloride is 153.81 amu. Since you also know that there are 6.022 × 1023 molecules per mole, you can calculate the mass of one mole of carbon tetrachloride as follows:
However, this result is not very useful in the lab. Laboratory balances are designed to measure mass in grams, not in atomic mass units. So, you can convert the mass to grams as shown below:
Thus, one molecule of carbon tetrachloride has a mass of 153.81 amu and one mole of carbon tetrachloride has a mass of 153.81 grams. The mass in grams per mole of a substance is called the molar mass and is denoted as M. The unit used for molar mass is grams per mole, g/mol. Notice that molar mass is numerically equal to the molecular mass.
To find the molar mass of a substance, follow the same procedure used for finding molecular mass. Thus, the molar mass for water is:
mass of one mole of oxygen + 2×(mass of one mole of hydrogen) = mass of one mole of water
16.00 g + 2 × 1.01 g = 18.02 g
Therefore, the molar mass of water is 18.02 g/mol.
Q
What is the mass, m, of one molecule of oxygen, O2?
[O = 16]
m =
answer :
32
Response:
That's the correct answer
Q
What is the molecular mass, M, of one molecule of oxygen, O2?
[O = 16]
M =
answer :
32
Response:
That's the correct answer
Q
What is the molar mass, M, of carbon dioxide, CO2?
[C = 12; O = 16]
M =
answer :
44
Response:
That's the correct answerUsing Molar Mass as a Unit Converter
Chemists use molar mass frequently to convert moles to grams and grams to moles. The following expression for molar mass can be applied to both cases:
M=mn
where n represents the number of moles, m the mass in grams and M the molar mass in g/mol. If you have a known number of moles of a substance and you want to find the mass in grams, you multiply the molar mass of the substance by the number of moles to find the mass in grams.
m=M×n
For example, if you have 2.4 moles of carbon tetrachloride, the following calculation could be used to determine how many grams this corresponds to.
In case the mass of a substance is known and you need to find the number of moles, you can use the relationship shown below:
Figure 22 After measuring the mass of a pure substance on a lab balance, a chemist can calculate how many moles
are present in the sample using the molar mass of the substance. Both solids and liquids can be measured this way.
Thus, if you had 65 grams of carbon tetrachloride, you could use the expression above to determine how many moles this corresponds to.
What is the mass, m, of 0.5 mol of ammonia, NH3?
[N = 14; H = 1]
[N = 14; H = 1]
m =
Molar Volume of a Gas
While the masses of solids and liquids can be easily measured using a laboratory balance, gases are more easily measured by their volumes. Thus, for gases, chemists often use a value known as molar volume to make quantitative measurements of molar amounts. Molar volume, denoted Vm, is the volume of one mole of gas, usually expressed in dm3/mol or L/mol. This is sometimes represented in the form shown below, where V is volume in liters and n is the number of moles of gas.
Vm=Vn
Unlike solids and liquids, gases do not have a fixed volume. Gases take the volume of their container. Moreover, the volume of a given amount of a gas depends on its temperature and pressure. Based on Avogadro’s hypothesis, at the same conditions of temperature (0°C) and pressure (1 atm), 22.4 dm3 (or 22.4 L) of any gas contain the same number of particles. This number was determined experimentally and found to be equal to 6.022 × 1023. In other words, at 0°C and 1 atm, 4 g of He, 28 g of N2, and 16 g of CH4 occupy the same volume, which is 22.4 dm3, and each contains 6.02 × 1023 particles.
Avogadro’s hypothesis has been supported by evidence collected for a large number of different gases. Thus, it has been shown over and over again that different gases have the same molar volume when measured at the same temperature and pressure.
To standardize conditions of temperature and pressure, chemists established standard temperature and pressure, abbreviated STP, as 0°C and 1 atm pressure. At STP, the molar volume of any gas is 22.4 L/mole. Be aware that this is the molar volume for most gases, especially gases with small molecules, including all the gaseous elements. Gases with larger molecules may have a slightly different molar volume. Also note that molar volumes of gases begin to vary beyond three significant figures.
Figure 23 At STP, one mole of any gas has a volume of 22.4 liters.
Q
What is the volume, V, 6.02 × 1023 atoms of helium gas at STP conditions?
[He = 4]
Give your answer to three significant figures.
V =
L
Using Molar Volume as a Unit Converter
Chemists use molar volume to find the number of moles in a given volume of gas. They also use molar volume to find the volume of a given number of gas moles. In other words, molar volume can be used to convert between number of moles and volume of a gas.
If you want to find the volume of a given number of moles of a gas, you can rearrange the expression above as follows:
V=Vm×n
For example, suppose a chemist wants to use 0.300 moles of methane gas for an experiment. The molar volume can be used to calculate the volume corresponding to this number of moles at STP. In this case, the molar volume at STP is multiplied by the number of moles needed.
This volume of gas would have to be measured under standard temperature and pressure conditions.
If you have a known volume of a gas and you want to find the number of moles of the gas, rearrange the expression as follows:
n=VVm
For example, if you had 0.295 liters of a gas under standard temperature and pressure conditions (STP), you can find the number of moles of gas in the sample by dividing the volume of the gas by its molar volume at STP.
In the examples above, the conditions were specified as STP conditions. The molar volume, 22.4 liters/mole, is relevant for these conditions,but not for other conditions. If temperature and pressure are not at STP, the molar volume will no longer be 22.4 liters/mole. The molar volume at the new conditions will have to be determined. For example, the molar volume at room temperature and pressure (25°C and 1 atm) is 24.4 liters/mole.
Q
Fill in the blank.
How many moles are present in 44.8 L of hydrogen gas at room temperature and pressure?
Give your answer to three significant figures.
number of moles =
mol
Reaction Stoichiometry
Generating oxygen for the astronauts aboard the International Space Station (ISS) had long been an issue that had to be dealt with before sending humans to outer space. If scientists have a chemical reaction that produces oxygen as a product, they can calculate how much reactant has to be carried on board the ISS to supply the necessary quantity of oxygen.
Calculations like the ones needed for determining oxygen quantities on board the ISS require that you know the balanced chemical equation for the reaction involved. Balancing the chemical equation for a reaction, by placing the appropriate coefficients in front of each reactant and product, assumes the validity of the law of conservation of mass.
The coefficients in front of the reactants and products in a balanced equation supply information about the reaction stoichiometry. Stoichiometry indicates the numerical relationships between reactants and products in a chemical reaction. These relationships allow you to use known quantities of one reactant or product in a reaction to calculate quantities of other reactants or products in the reaction.
For example, oxygen is generated on the ISS by the following chemical reaction:
From this, a chemist would say that there is a 2:1 stoichiometric ratio of water to oxygen and a 2:2 stoichiometric ratio of water to hydrogen in this reaction. Thus, the coefficients of the balanced equation provide the stoichiometric ratios between reactants and products. For cases such as the 2:2 ratio, you can simplify and say that the stoichiometric ratio is 1:1.
Furthermore, based on the law of conservation of mass, the mass of water decomposed is the same as the total mass of hydrogen gas and oxygen gas produced. In the above example, we know that the mass of one mole of water is 18 g, that of hydrogen is 2 g, and that of oxygen is 32 g. Therefore, we can use the balanced equation to deduce the mass ratios relating reactants and products:
Q
Given the following reaction:
2NH3 → N2 + 3H2
Determine the stoichiometric ratio between the reactants and the products in the reaction above.
The stoichiometric ratio of ammonia to hydrogen is 3:2.
The stoichiometric ratio of ammonia to nitrogen is 1:2.
The stoichiometric ratio of ammonia to hydrogen is 2:3.
The stoichiometric ratio of ammonia to nitrogen is 2:1.
Stoichiometric Calculations
Suppose you were in charge of supplying the space station with the materials needed for generating oxygen for the astronauts to breathe. For a crew of six, a total volume of 750 liters of oxygen at 25°C and 1 atm will be sufficient for one day.
What materials would you supply and how much of these materials would be needed? To find out, you could use the balanced chemical equation for the reaction that generates oxygen and carry out some stoichiometric calculations. The space station has an oxygen generator that operates using the following chemical reaction:
From this, you know that water is the raw material needed for the production of oxygen in the space station. The question is how much water do you need to supply six astronauts with one day’s worth of oxygen?
Figure 24 Russian cosmonaut Yury I. Onufrienko performs maintenance
on the oxygen generating system aboard the ISS.
You know that you need 750 liters of oxygen at 25°C and 1 atm. To find the number of moles of a gas in a certain volume of that gas we use the relation below.
Thus, the number of moles of oxygen gas present in 750 L of that gas is:
Now you know that you need 30.74 moles of oxygen. The next step is to use this information to find the moles of water that will produce this amount of oxygen. The balanced chemical equation tells you that 2 moles of water produce 1 mole of oxygen. You can use this stoichiometric ratio as a conversion factor to convert moles of oxygen to moles of water:
Once you have calculated the number of moles of water, you can use this value and the molar mass of water to find the mass of water. Knowing the mass of water will allow you to measure the water needed for each day’s supply of oxygen. To find the mass of water we can use the relation below.
Thus, you need to supply a crew of six aboard the ISS with 1.11 kg of water per day for generating the necessary amount of oxygen for them to survive.
Now consider another problem that can be solved using stoichiometric principles. Two liquids, dinitrogen tetroxide (N2O4) and hydrazine (N2H4) are sometimes used as fuels to launch spacecraft from Earth. When these two liquids are combined, they react to produce nitrogen gas (N2) and water vapor (H2O). Some rockets require the formation of 2.00 × 104 moles of nitrogen gas to achieve liftoff. The problem is to find the mass of hydrazine (N2H4) that should be supplied to launch the spacecraft.
Given: number of moles of N2 , n = 2.00 × 104 mol
Required to find: mass of N2H4 , m = ?
The first step is to balance the equation for the chemical reaction.
Next, use the balanced equation to determine the mole ratios of reactants and products.
The stoichiometric ratio of hydrazine to nitrogen is a 2 to 3 molar ratio. Using this ratio, you can convert the moles of nitrogen produced to moles of hydrazine needed by multiplying the ratio by the moles of nitrogen:
The moles of hydrazine can be converted to grams using its molar mass. Calculate the molar mass by adding the atomic masses of all of the atoms present in one molecule of hydrazine:
M of N2H4 = (2× 14.01) + (4 × 1.01) = 32.06 g/mol
Multiply the moles of hydrazine by its molar mass to find the mass of hydrazine:
Consider another problem. Solid potassium chlorate (KClO3) decomposes to form solid potassium chloride (KCl) and oxygen gas (O2). If an amount of 20.0 grams of potassium chlorate is completely decomposed, what volume of oxygen gas is produced at STP?
Given: mass of KClO3 = 20.0 g
M of KClO3 = 122.55 g/mol
Required to find: V of O2 produced = ?
Begin by writing the balanced chemical equation of the reaction.
The moles of KClO3 can be calculated using the expression:
n=mM
Then, write the ratios of the reactants and products in terms of moles.
You can use the moles of KClO3 that decompose to find the moles of oxygen produced using the stoichiometric information from the balanced equation. The balanced equation shows that three oxygen molecules form for every two molecules of KClO3 that decompose. Thus, the molar ratio of O2 to KClO3 is 3 to 2. Using this ratio, you can convert the moles of KClO3 decomposed to moles of O2 produced by multiplying the ratio by the moles of KClO3:
Finally, you can use the molar volume of gases at STP to convert the moles of O2 produced to volume of O2 produced knowing that the molar volume of gases at STP is 22.4 L/mol.
Q
Consider the following reaction:
2Mg + O2 → 2MgO
What is the volume, V, of air needed to burn 2.0 g of magnesium at STP conditions?
[Mg = 24; O = 16]
V =
L
Q
Consider the following reaction:
2SO2 + O2 → 2SO3
What is the mass of SO3 produced when 0.25 mol of O2 reacts completely with SO2?
[S = 32; O = 16]
40 g
20 g
0.5 g
30 g
End of Chapter 4
Back to the Main Menu